SISTEMA DE COORDENADAS RECTANGULARES
un sistema coordenado en el plano es un sistema coordenado en el cual un punto puede moverse en todas direcciones manteniéndose siempre en un plano o sistema bidimencional y es utilizado en la geometría plana.
el ejemplo que estudiaremos de estos sistemas, y, ademas, el mas importante, es el sistema coordenado rectangular.
 |
| sistema coordenado rectangular |
este sistema, consta de:
- dos rectas Y'Y y X'X, llamadas ejes de coordenadas ,perpendiculares entre si.
- la recta X'X se llama eje X o eje de abscisas y la recta Y'Y se llama eje Y o eje de ordenadas; y su punto de intersección 0 se llama origen
- los ejes de coordenadas dividen el plano en 4 regiones llamadas cuadrantes
- la dirección positiva del eje X es hacia la derecha y la del eje Y es hacia arriba
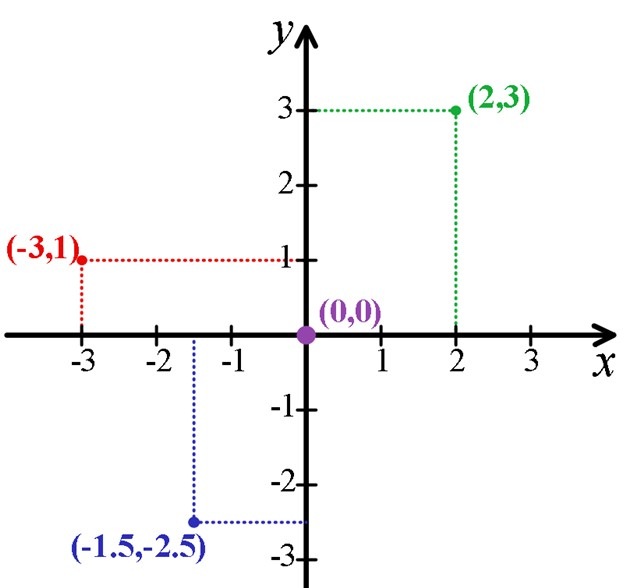
el procedimiento para localizar un punto en el plano a través del sistema rectangular es sencillo:
- la forma de representar las coordenadas de un punto P es colocar el literal del punto en este caso P. antecediendo a un paréntesis donde se ubican primero el valor de la abscisa y después el de la ordenada de dicho punto separadas por una coma, así: P(x,y).
Para localizar la abscisa o valor de x, se cuentan las unidades correspondientes hacia la derecha si son positivas o hacia a izquierda si son negativas, a partir del punto de origen, en este caso el cero.
Desde donde se localiza el valor de x, se cuentan las unidades correspondientes hacia arriba si son positivas o hacia abajo, si son negativas y de esta forma se localiza cualquier punto dadas sus coordenadas.
1. represente con coordenadas rectangulares los puntos en la siguiente imagen:
2. represente con coordenadas rectangulares los puntos en la siguiente imagen:
3.represente con coordenadas rectangulares los puntos en la siguiente imagen:
4. represente en el plano las siguientes coordenadas:
F(3,-5)
G(-4,6)
E(-3,0)
D(-1,-2)
C(4,0)
B(1,-4)
A(3,5)
